ストップオーバーの「場合の数」 【マレーシア航空準世界一周チケットを題材に】
その昔マレーシア航空が準世界一周チケットを販売していた。
ルートは「日本→マレーシア→南アフリカ→アルゼンチン」と「米国→日本」(もちろん逆の東回りもOK)で、「準」が付くのは南米-北米間に同社の路線がなく、別途手配を要したため。
幾度か購入しかけたものの、残念ながら世界一周は叶わなかった。
代わりに、現在このチケットが買えたら、どんな旅程を組むかを想像する。
南アフリカはヨハネスブルグとケープタウンの両方に寄れたはずだが、これらをまとめて国単位で考えるとストップオーバー(途中降機)可能な国は、マレーシア、南アフリカ、アルゼンチン、米国の4つだ。追加手配の「アルゼンチン→米国」をパナマ経由とし、そこでもストップオーバーすれば最大で5ヶ国に滞在できる。
では、訪問国の組み合わせは何通りあるか?
普通は誰もが、5ヶ国すべてに立ち寄る。わざわざこんなチケットを買う以上、それが当然だ。
反対の極端な例として、どこにも降機せずに帰国、つまり出入国ゼロも(フライトスケジュール次第で)あり得る。マイレージ修行とか、今なら空港のラウンジ巡りといった目的が想定される。
ほかに、危険な国を避けた結果、3ヶ国もしくは4ヶ国に落ち着くことも多いだろう。
また、形ばかりでも世界一周したいが、時間の制約で1ヶ国かせいぜい2ヶ国に絞るというのもなくはない。
5ヶ国すべてに立ち寄るのと、出入国ゼロは各々1通り。1ヶ国だけはマレーシアのみ、南アフリカのみ、…と5通りある。4ヶ国はスルーの国が1ヶ国と解し5通り。
2ヶ国のパターンは、はじめに5ヶ国から1つ選ぶのが5通り、続いて残りの4ヶ国のうちでもう1つ選ぶのが4通り。よって5×4=20になりそうだが、この値は最初に選んだ国と2回目に選んだ国が逆のケースも含んでいるので、2で割って10通り。3ヶ国だとスルーの国が2ヶ国と見て10通り。
整理すると、全部で32通りだ。
5ヶ国それぞれについてストップオーバーする/しないの2通りが選べるため、2の5乗=32と求めてもよい。
| 訪問国数 | 訪問国組み合わせ | 場合の数 |
| 0 | {} | 1 |
| 1 | {マ}{南}{ア}{パ}{米} | 5 |
| 2 |
{マ南}{マア}{マパ} {マ米}{南ア}{南パ} {南米}{アパ}{ア米} {パ米} |
10 |
| 3 |
{マ南ア}{マ南パ}{マ南米} {マアパ}{マア米}{マパ米} {南アパ}{南ア米}{南パ米} {アパ米} |
10 |
| 4 |
{マ南アパ}{マ南ア米} {マ南パ米}{マアパ米} {南アパ米} |
5 | 5 | {マ南アパ米} | 1 |
次にちょっとややこしくなるが、各国に泊まる日数が計10日(機中泊は除外)のとき、旅程が何通りあるかを考える。実際は違ったが、フライトは全区間で毎日就航と仮定。
西回りに限ると、最初に日本からマレーシアに飛ぶのと、10泊後に米国から日本に飛ぶのは確定している(下図の赤線)。したがって、マレーシア到着(下図のA)から米国発のフライトに乗る(下図のB)までの間の、4区間の空間移動(下図の横方向)と10日間の時間の流れ(下図の縦方向)の組み合わせを数えればよさそうだ。
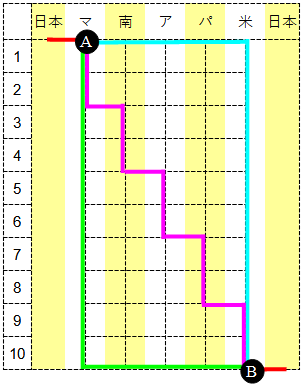
緑色の線はマレーシアでずっと過ごし最終日にぐるっと西回り、水色の線は初日に米国まで一気に西へ飛びそこに滞在、ピンク色の線は各国に満遍なく2泊ずつという旅程を表す。
AからBに至るには、右(→)に計4ステップ、下(↓)に計10ステップの総計14ステップの移動が必要。空間も時間も後戻りNGで、上と左へは進めない。よって、14ステップ中に4つの→の配置が何通り可能かで、経路の数が求まる。水色の線は→を14ステップ中最初の4ステップに(→→→→↓↓…↓)、緑色の線は11から14ステップ目(↓↓…↓→→→→)、ピンク色の線は3、6、9、12ステップ目に割り当てている。
最初に→を置く際は、14ステップ中の1つを自由に選べる。次は最初に決めたところ以外の残り13ステップのどこか…と順々に考え、4つの→の配置は14×13×12×11で24,024通りか。いや、膨大すぎる。例えば→を2、4、6、8ステップ目に置くとき、先の計算では最初の→で8ステップ目を選ぶ手順も、2番目の→で8ステップ目を選ぶ手順も数えてしまう。選んだ順で並べた結果が「8246」だろうが「2846」だろうが経路は等しく、これらの区別は無用。
重複分がどのくらいかは、2、4、6、8を使い4桁の数字が何通り作れるかと捉えることができる。1桁目は4通り、2桁目は3通り、…で、4×3×2×1=24だ。すべての4つのステップの組み合わせが24ずつの重複ゆえ、答えは24,024÷24=1,001になる。
東周りも含めると、倍の2,002だ(航空券の内容を脇に置き、宿泊地だけに注目すれば、1ヶ国に10連泊は西回りも東回りも同じため、5を引いて1,997)。
題材を変える。
日本を発ちクアラルンプールに着き、観光しながら南下し、シンガポールから帰る計画を立てた。期間は平日5日の連続休暇と前後の週末を合わせた8泊9日で、滞在(宿泊)予定はクアラルンプール、マラッカ、ジョホールバル、シンガポールの4都市。
上記の順に4都市を8泊で巡る旅程は何通りあるか?
今回は都市をスルーせず、すべてに必ず泊まる。つまり、仮に世界のどのホテルでも使えるバウチャーが8泊分で8枚あるとすれば、4都市のホテル各々に最低1枚ずつはそれを渡す。したがって、最初に4枚を取り除き、残りの4枚をどう4都市に分けるかの問題だ。
そこで、準世界一周のときの方法で、4都市(3区間)・4泊の組み合わせを求める。→3つ+↓4つの計7ステップに→3つを配置するのは、7×6×5÷(3×2×1)で35通り。
取り除いておいた4都市1泊ずつを戻すと、例えば4泊が{クママジ}(各都市の先頭1文字で表記)だと{ククマママジジシ}だし、{クシシシ}は{ククマジシシシシ}だ。
月並みな定番ルート、かつ会社員の長期(?)休暇でお決まりの8泊9日でも、35通り(イン・アウト逆も足すと70通り)にも散らばるのなら、きっとオリジナルな旅ができるはず。
しかし、いざ来るとマラッカあたりで「あの人、日本からの飛行機で見たな」と思しき日本人と目が合い、ジョホールバルで同じ人物とすれ違い、照れながら会釈し、シンガポールの空港で再び出くわし、互いに観念してぎこちなく言葉を交わす…というような事態は起こり得る。
いや、起こり得た。
こんなのは、それこそマレーシア航空準世界一周チケットが買えた時代に最もよく聞いた過去の話だ。
以前はどこも東洋系の外国人旅行者といえば日本人だったのに、今や似た顔立ちの他国の旅行者の台頭が著しい。日本人がいても目立たないし、現地の人々の我々に対する接し方もかなり変化した。
なので、もう自分だけの旅なんて意識せずに、かつての王道ルートのど真ん中を進んでも、同胞と会って面映ゆさを感じる心配はおそらく杞憂に終わる。喜ぶべきか、悲しむべきか、功罪相半ばか。
いずれにせよ、日本人旅行者が踏み固めた道を辿る旅は、もはや稀有になった。